遍历二叉树

前序遍历

规则是若二叉树为空，则空操作返回，否则先访问跟结点，然后前序遍历左子树，在前序遍历右子树。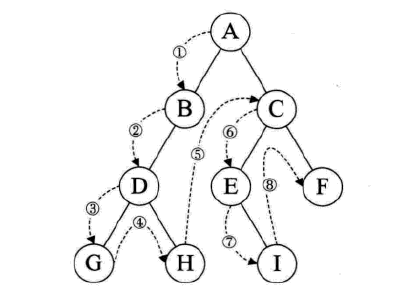

/* 二叉树的前序遍历递归算法 */
void PreOrderTraverse (BiTree T){
  if (T==NULL) {
    return;
  }
  printf ("%c", T->data); /* 显示结点数据，可以更改为其他对结点操作 */
  PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
  PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}

中序遍历

规则是若二叉树为空，则空操作返回，否则从跟结点开始（并不是先访问根结点），中序遍历根结点的左子树，然后是访问右子树，最后中序遍历右子树。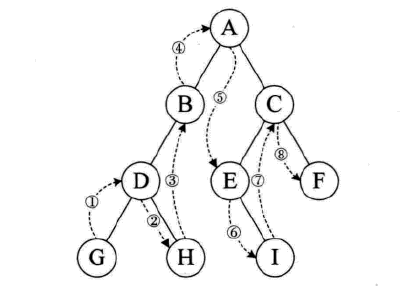

/* 二叉树的中序遍历递归算法 */
void InOrderTraverse (BiTree T){
  if (T==NULL) {
    return;
  }
  InOrderTraverse(T->lchild); /* 中序遍历左子树 */
  printf ("%c", T->data); /* 显示结点数据，可以更改为其他对结点操作 */
  InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}

后序遍历

规则是若二叉树为空，则空操作返回，否则从左到右先子叶后结点的方式遍历访问左右子树，最后事访问根结点。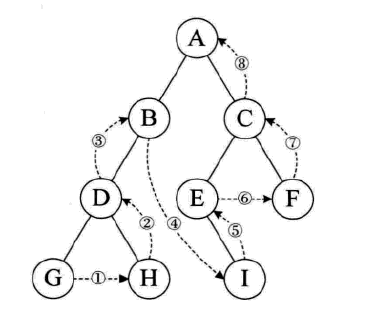

/* 二叉树的后序遍历递归算法 */
void PostOrderTraverse (BiTree T){
  if (T==NULL) {
    return;
  }
  PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */
  PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */
  printf ("%c", T->data); /* 显示结点数据，可以更改为其他对结点操作 */
}

层序遍历

规则是若二叉树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。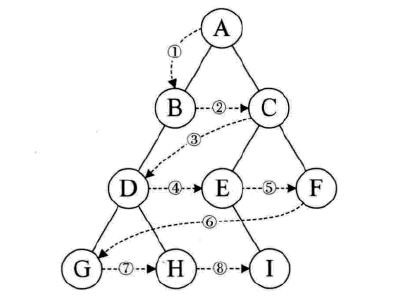

推到遍历结果

已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知前序遍历序列和后序遍历序列，不能确定一棵二叉树。

二叉树的建立

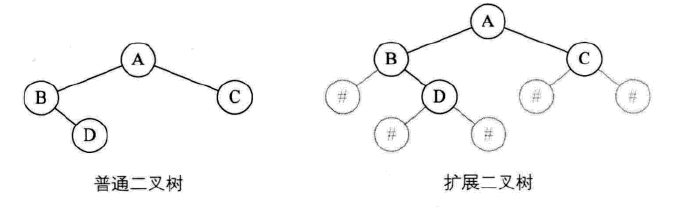
前序序列 AB#D##C##，用键盘挨个输入。实现的算法如下：

/* 按前序输入二叉树中结点的值（一个字符） */
/* #表示空树，构造二叉链表表示二叉树T。 */
void CreateBiTree (BiTree *T) {
  TElemType ch;
  scanf("%c", &ch);
  if (ch=='#'){
    *T=NULL;
  }else{
    *T=(BiTree)malloc(sizeof(BiTNode));
    if(!*T){
      exit(OVERFLOW);
    }
    (*T)->data=ch; /* 生成根结点 */
    CreateBiTree(&(*T)->lchild); /* 构造左子树 */
    CreateBiTree(&(*T)->rchild); /* 构造右子树 */
  }
}

线索二叉树

中序遍历时得到 HDIBJEAFCG 这样的序列，可以知道结点 I 的前驱是 D，后继是 B。
指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树（Threaded Binary Tree）。