定义

二叉树（Binary Tree）是 $n(n≥0)$个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树组成。

特点

• 每个结点最多有两颗子树
• 左子树和右子树是有顺序的
• 即使树中某个结点只有一颗子树，也需要区分它是左子树还是右子树。

五种基本形态

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
• 根结点只有右子树
• 根结点既有左子树又有右子树

特殊二叉树

• 斜树
  所有的结点都只有左子树的二叉树叫左斜树。所有的结点都只有右子树的二叉树叫右斜树。这两者统称为斜树。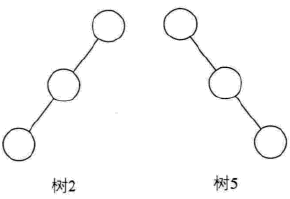
  
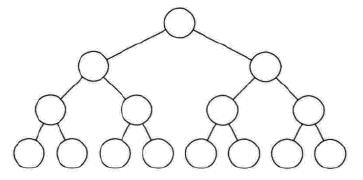
• 满二叉树
  在一棵二叉树中，如果所有的分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
  满二叉树特点：
  • 叶子只能出现在最下一层
  • 非叶子结点的度一定是2
  • 同样深度的二叉树树中，满二叉树的结点个数最多，叶子数最多。
    
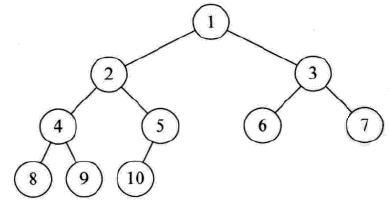
• 完全二叉树
  对一棵具有 n 个结点的二叉树按层序编号，如果编号为 $i(1≤i≤n)$ 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树的位置完全相同，则这棵二叉树称为完全二叉树。
  满二叉树一定是一棵完全二叉树，但完全二叉树不一定是满二叉树。
  完全二叉树特点：
  • 叶子结点只能出现在最下两层
  • 最下层的叶子一定集中在左部连续位置
  • 倒数二层，若有叶子结点，一定都在右部连续位置
  • 如果结点度为 1，则该结点只有左孩子，既不存在只有右子树的情况
  • 同样结点数的二叉树，完全二叉树的深度最小
    

二叉树的性质

1. 在二叉树的第 i 层上至多有 $2^{i-1}$ 个结点 $(i≥1)$
2. 深度为 k 的二叉树至多有 $2^k-1$ 个结点 $(k≥1)$
3. 对任何一棵二叉树 T，如果其终端结点数为 $N_0$，度为 2 的结点数为 $N_2$，则 $N_0=N_2+1$。
4. 具有 n 个结点的完全二叉树的深度为「$log_2 n$」$+1$ (「x」表示不大于 x 的最大整数)。
5. 如果对一棵有 n 个结点的完全二叉树（其深度为「$log_2 n$」$+1$）的结点按层序编号（从第 1 层到第「$log_2 n$」$+1$层，每层从左到右），对任一结点 $i （1≤i≤n）$有：
   1. 如果 $i=1$，则结点 $i$ 是二叉树的根，无双亲；如果 $i＞1$，则其双亲是结点「$i/2$」。
   2. 如果 $2i>n$，则结点 $i$ 无左孩子（结点 $i$ 为叶子结点）；否则其左孩子是结点 $2i$。
   3. 如果 $2i+1>n$，则结点 $i$ 无右孩子；否则其右孩子是结点 $2i+1$。

二叉树的存储结构

二叉树顺序存储结构

顺序存储结构一般只用于完全二叉树。如果不是完全二叉树会造成空间的浪费。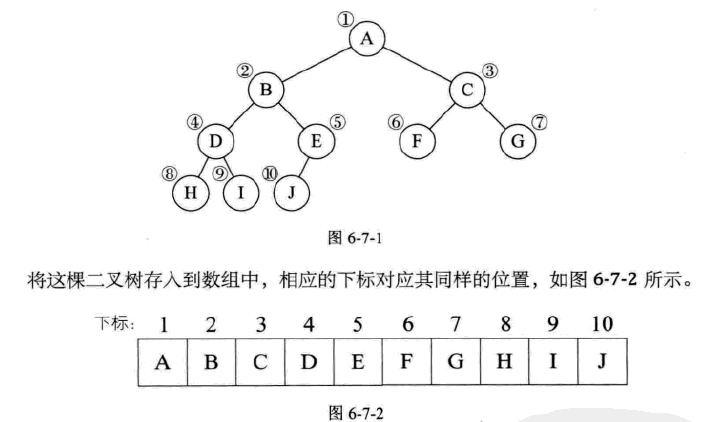

二叉链表

data 是数据域。
lchild 和 rchild 都是指针域，分别存放左右孩子的指针。

/* 二叉树的二叉链表结点结构定义 */
typedef struct BiTNode /* 结点结构 */ {
    TElemType Data; /* 结点数据 */
    struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
} BiTNode, *BiTree;