《大话数据结构》笔记03-线性表

线性表

线性表：零个或多个数据元素的有限序列。

线性表的抽象数据类型定义如下：

ADT 线性表(List)
Data
    线性表的数据对象集合为{a1, a2, ... , an}，每个元素的类型均为DataType。其中，除第一个元素a1外，每个元素有且仅有一个直接前驱元素，除了最后一个元素an 外，每一个元素有却仅有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation
    InitList(*L): 初始化操作，建立一个空的线性表L。
    ListEmpty(L): 若线性表为空，返回true，否则返回false。
    ClearList(*L): 将线性表清空。
    GetElem(L, i, *e): 将线性表L中的第i个位置元素值返回给e。
    LocateElem(L, e): 在线性表L中查找于给定值e相等的元素，如果查找成功，返回该元素在表中的序号表示成功；否则，返回0(-1)表示失败。
    ListInsert(*L, i, e): 在线性表L中的第i个位置插入新元素e。
    ListDelete(*L, i, e): 删除线性表L中第i个位置元素，并用e返回其值。
    ListLength(L)： 返回线性表L的元素个数。
endADT

Java中 List<E> 接口中部分方法：

public interface List<E> extends Collection<E> {
    //返回列表中的元素数。
    int size();
    //如果列表不包含元素，则返回 true。
    boolean isEmpty();
    //从列表中移除所有元素
    void clear();
    //如果列表包含指定的元素，则返回 true。
    boolean contains(Object o);
    //向列表添加指定的元素
    boolean add(E e);
    void add(int index, E element);
    E remove(int index);//删除
    boolean remove(Object o);//从此列表中移除第一次出现的指定元素（如果存在）

    E get(int index);
    E set(int index, E element);
    int indexOf(Object o);
    int lastIndexOf(Object o);
}

线性表的顺序存储结构

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

线性表的顺序存储的结构代码：

#define MAXSIZE 20  /* 存储空间初始分配量 */
typedef int ElemType; /* ElemType 类型根据实际情况而定，这里假设为int */
typedef struct｛
    ElemType data[MAXSIZE]; /* 数组存储数据元素，最大值为MAXSIZE */
    int length; /* 线性表当前长度 */
｝SqList;

顺序存储结构需要三个属性：

• 存储空间的起始位置：数组 data，它的存储位置就是存储空间的存储位置。
• 线性表的最大存储容量：数组长度 MAXSIZE。
• 线性表的当前长度：length。

对每个线性表位置的存入或者取出数据，时间复杂度为$O(1)$，我们通常把具有这一特点的存储结构称为随机存取结构。

顺序存储结构的插入操作

思路：

• 如果插入位置不合理，抛出异常；
• 如果线性表长度大于数组长度，则抛出异常或动态增加容量；
• 从最后一个元素向前遍历到第i个位置，分别将它们都向后移动一个位置；
• 将要插入的元素填入位置i处；
• 表长加1.

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
/* Status是函数的类型，其值是函数结果状态代码，如OK等 */
typedef int Status;

/* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
Status ListInsert(SqList *L, int i, ElemType e){
    int k;
    if (L->length == MAXSIZE) /* 顺序线性表已经满 */
        return ERROR;
    if (i < 1 || i > L->length + 1) /* 当i不在范围内时 */
        return ERROR;
    if (i <= L->length) { /* 若插入的数据的位置不在表尾 */
        for (k = L->length - 1; k >= i - 1; k--) { /* 将要插入位置后数据元素向后移动一位 */
            L->data[k+1] = L->data[k];
        }
    }
    L->data[i-1] = e; /* 将新元素插入 */
    L->length++;
    return OK;
}

顺序存储结构的删除操作

思路：

• 如果删除的位置不合理，抛出异常；
• 取出删除的元素；
• 从删除元素的位置开始遍历到最后一个元素的位置，分别将它们都向前移动一个位置；
• 表长减1。

插入和删除操作的时间复杂度为$O(n)$

线性表顺序存储结构的优缺点

线性表的链式存储结构

为了表示每个数据元素$a_i$与其直接后继数据元素$a_{i+1}$之间的逻辑关系，对数据元素$a_i$来说，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素谢谢的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素$a_i$的存储映像，称为结点（Node）。

n个结点($a_i$的存储映像)链结成一个链表，即为线性表（$a_1, a_2, ..., a_n$）的链式存储结构，因为此链表的每一个结点中只包含一个指针域，所以叫做单链表。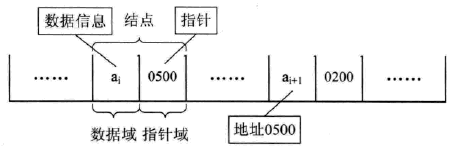

链表中第一个结点的存储位置叫做头指针，最后一个结点指针为NULL(或用"^"符号表示)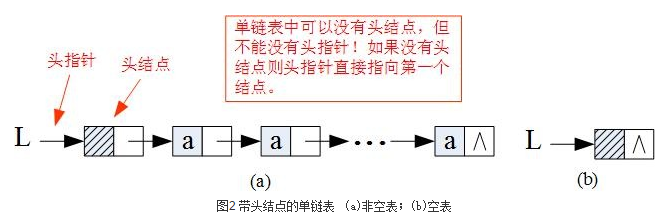

头指针与头结点的异同

线性表的单链表存储结构代码描述

typedef struct Node{
    ElemType data;
    struct Node *next;
} Node;
typedef struct Node *LinkList; /* 定义LinkList */

单链表的读取

思路：

1. 声明一个结点$p$指向链表第一个结点，初始化$j$从1开始；
2. 当$j<i$时，就遍历链表，让$p$的指针向后移动，不断指向下一个结点，$j$累加1；
3. 若到链表末尾$p$为空，则说明第$i$个元素不存在；
4. 否则查找成功，返回结点$p$的数据。

时间复杂度是$O(n)$。

单链表的插入与删除

单链表插入和删除算法，我们发现，它们其实都是由两部分组成：第一部分就是遍历查找第$i$个结点；第二部分就是插入和删除结点。我们很容易推导出：它们的时间复杂度都是$O(n)$。如果在我们不知道第i个结点的指针位置，单链表数据结构在插入和删除操作上，与线性表的顺序存储结构是没有太大优势的。我们只需要在第一次时，找到第$i$个位置的指针，此时为$O(n)$，接下来只是简单地通过赋值移动指针而已，时间复杂度都是$O(1)$。显然，对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显。

单链表结构与顺序存储结构优缺点

静态链表

静态链表其实是为了给没有指针的高级语言设计的一种实现单链表能力的方法。
用数组描述的链表叫做静态链表。

为了我们方便插入数据，通常会把数组建立得大一些，以便有一些空闲空间可以便于插入时不至于溢出。

/* 线性表的静态链表存储结构 */
#define MAXSIZE 1000
typedef struct{
    ElemType data;
    int cur; /* 游标，为0时表示无指向 */
} Component, StaticLinkList[MAXSIZE];

另外我们对数组第一个和最后一个元素作为特殊元素处理，不存数据。我们通常把未被使用的数组元素称为备用链表。而数组第一个元素，即下标为0的元素的cur就存放备用链表的第一个结点的下标；而数组的最后一个元素的cur则存放第一个有数值的元素的下标，相当于单链表中的头结点作用，当整个链表为空时，则为0。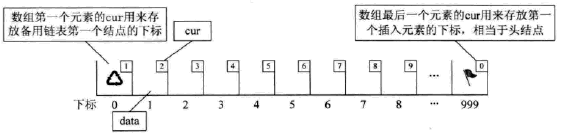

静态链表优缺点

优点：在插入和删除操作时，只需要修改游标，不需要移动元素，从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点。
缺点：①没有解决连续存储分配带来的表长难以确定的问题；②失去了顺序存储结构随机存取的特性。

循环链表

将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。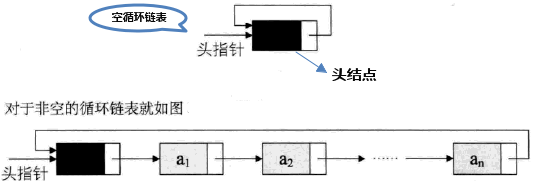

其实循环链表和单链表的主要差异就在与循环的判断条件上，原来是判断p->next是否为空，现在则是p->next不等于头结点，则循环未结束。

尾指针

终端结点用尾指针rear指示，则查找终端结点是$O(1)$，而开始结点，其实就是rear->next->next，时间复杂度也是$O(1)$。

要将两个循环链表合并成一个表时，有了尾指针就非常简单了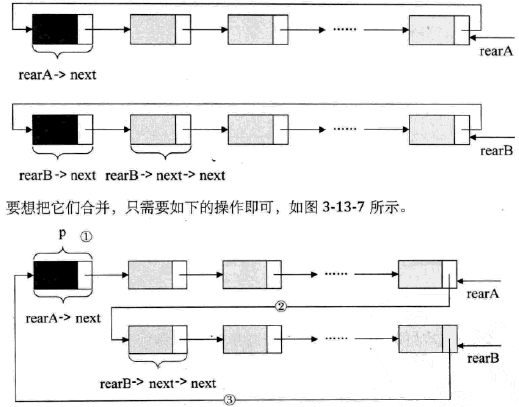

注意：只保留一个头结点

p=rearA->next;
rearA->next = rearB->next->next;
q = rearB->next;
rearB->next = p;
free(q);

双向链表

双向链表是在单链表的每一个结点中，在设置一个指向其前驱结点的指针域。

/* 线性表的双向链表存储结构 */
typedef struct DulNode{
    ElemType data;
    struct DulNode *prior; /* 直接前驱指针 */
    struct DulNode *next;  /* 直接后继指针 */
} DulNode, *DuLinkList;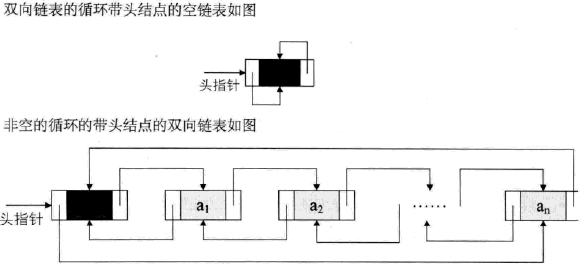

在插入和删除时，需要改变两个指针变量。

插入：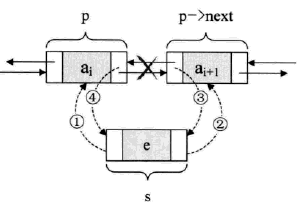

s->prior = p;
s->next = p->next;
p->next->proir = s;
p->next = s;

删除：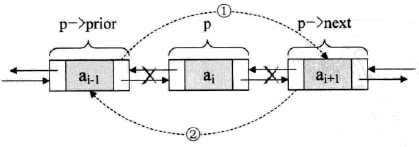

p->proir->next = p->next;
p->next->prior = p->prior;